znzcqy的博客

写在前面，大二生活刚开始，有点空闲时间，线性代数刚学完行列式，借此机会复习一下（手动滑稽）。

好的，计算行列式的方法相信大家都会，这里使用按行（列）展开（降阶法），不要问我为啥不用定义算，因为不会……

为了简化代码，这里只用第一列展开的结果，当然用任意列（行）步骤和结果都是一样的哈。那么就附上代码：

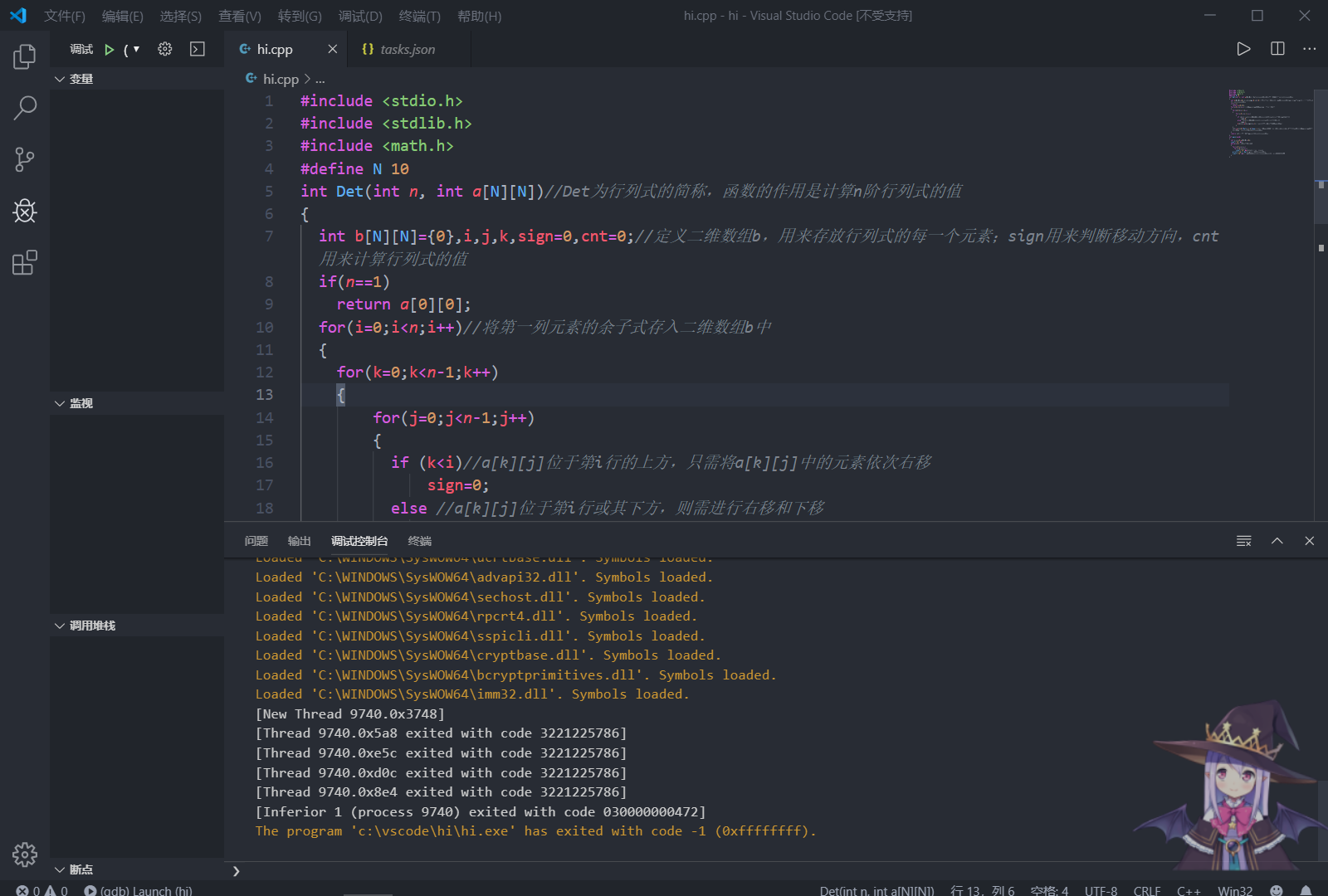
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define N 10
int Det(int n, int a[N][N])//Det为行列式的简称，函数的作用是计算n阶行列式的值
{
  int b[N][N]={0},i,j,k,sign=0,cnt=0;//定义二维数组b，用来存放行列式的每一个元素；sign用来判断移动方向，cnt用来计算行列式的值
  if(n==1)
    return a[0][0];
  for(i=0;i<n;i++)//将第一列元素的余子式存入二维数组b中
  {
    for(k=0;k<n-1;k++)
    {
        for(j=0;j<n-1;j++)
        {
          if (k<i)//a[k][j]位于第i行的上方，只需将a[k][j]中的元素依次右移
              sign=0;
          else //a[k][j]位于第i行或其下方，则需进行右移和下移
              sign=1;
          b[k][j]=a[k+sign][j+1];//执行移动操作，实现余子式的存储
        }
    }
    cnt+=a[i][0]*Det(n-1,b)*pow(-1,i);//余子式的系数为-1的i+j次方，而j=0；使用递归，将第一列元素的代数余子式之和存入cnt，cnt的值即为行列式的值
  }
  return cnt;//函数的返回值cnt即为n阶行列式的值
}
int main(void)
{
  int i,j,n=0,a[N][N]={0}; 
  scanf("%d",&n);
  while(n>0)//n的值必须大于0
  {
    for(i=0;i<n;i++)
      for(j=0;j<n;j++)
        scanf("%d",&a[i][j]);//读入行列式
    printf("%d\n",Det(n,a));//输出行列式的值
    scanf("%d",&n);//可以连续计算多个行列式的值，直到n<=0时结束程序
  }
}

最后贴上一张图片，成功水完一篇博客